Game theory

2007 Schools Wikipedia Selection. Related subjects: Mathematics

Game theory is a branch of applied mathematics and economics that studies situations where players choose different actions in an attempt to maximize their returns. First developed as a tool for understanding economic behaviour and then by the RAND Corporation to define nuclear strategies, game theory is now used in many diverse academic fields, ranging from biology and psychology to sociology and philosophy. Beginning in the 1970s, game theory has been applied to animal behaviour, including species' development by natural selection. Because of games like the prisoner's dilemma, in which rational self-interest hurts everyone, game theory has been used in political science, ethics and philosophy. Finally, game theory has recently drawn attention from computer scientists because of its use in artificial intelligence and cybernetics.

In addition to its academic interest, game theory has received attention in popular culture. A Nobel Prize-winning game theorist, John Nash, was the subject of the 1998 biography by Sylvia Nasar and the 2001 film A Beautiful Mind. Game theory was also a theme in the 1983 film WarGames. Several game shows have adopted game theoretic situations, including Friend or Foe? and to some extent Survivor. The character Jack Bristow on the television show Alias is one of the few fictional game theorists in popular culture.

Although similar to decision theory, game theory studies decisions that are made in an environment where various players interact. In other words, game theory studies choice of optimal behaviour when costs and benefits of each option are not fixed, but depend upon the choices of other individuals.

Representation of games

The games studied by game theory are well-defined mathematical objects. A game consists of a set of players, a set of moves (or strategies) available to those players, and a specification of payoffs for each combination of strategies. There are two ways of representing games that are common in the literature.

See also List of games in game theory.

Normal form

	Player 2 chooses Left	Player 2 chooses Right
Player 1 chooses Up	4, 3	–1, –1
Player 1 chooses Down	0, 0	3, 4
Normal form or payoff matrix of a 2-player, 2-strategy game

The normal (or strategic form) game is a matrix which shows the players, strategies, and payoffs (see the example to the right). Here there are two players; one chooses the row and the other chooses the column. Each player has two strategies, which are specified by the number of rows and the number of columns. The payoffs are provided in the interior. The first number is the payoff received by the row player (Player 1 in our example); the second is the payoff for the column player (Player 2 in our example). Suppose that Player 1 plays Up and that Player 2 plays Left. Then Player 1 gets a payoff of 4, and Player 2 gets 3.

When a game is presented in normal form, it is presumed that each player acts simultaneously or, at least, without knowing the actions of the other. If players have some information about the choices of other players, the game is usually presented in extensive form.

Extensive form

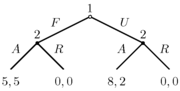
The extensive form can be used to formalize games with some important order. Games here are presented as trees (as pictured to the left). Here each vertex (or node) represents a point of choice for a player. The player is specified by a number listed by the vertex. The lines out of the vertex represent a possible action for that player. The payoffs are specified at the bottom of the tree.

In the game pictured here, there are two players. Player 1 moves first and chooses either F or U. Player 2 sees Player 1's move and then chooses A or R. Suppose that Player 1 chooses U and then Player 2 chooses A, then Player 1 gets 8 and Player 2 gets 2.

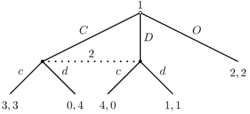
The extensive form can also capture simultaneous-move games. Either a dotted line or circle is drawn around two different vertices to represent them as being part of the same information set (i.e., the players do not know at which point they are).

Types of games

Symmetric and asymmetric

	E	F
E	1, 2	0, 0
F	0, 0	1, 2
An asymmetric game

A symmetric game is a game where the payoffs for playing a particular strategy depend only on the other strategies employed, not on who is playing them. If the identities of the players can be changed without changing the payoff to the strategies, then a game is symmetric. Many of the commonly studied 2×2 games are symmetric. The standard representations of chicken, the prisoner's dilemma, and the stag hunt are all symmetric games. Some scholars would consider certain asymmetric games as examples of these games as well. However, the most common payoffs for each of these games are symmetric.

Most commonly studied asymmetric games are games where there are not identical strategy sets for both players. For instance, the ultimatum game and similarly the dictator game have different strategies for each player. It is possible, however, for a game to have identical strategies for both players, yet be asymmetric. For example, the game pictured to the right is asymmetric despite having identical strategy sets for both players.

Zero sum and non-zero sum

	A	B
A	–1, 1	3, –3
B	0, 0	–2, 2
A zero-sum game

In zero-sum games the total benefit to all players in the game, for every combination of strategies, always adds to zero (more informally, a player benefits only at the expense of others). Poker exemplifies a zero-sum game (ignoring the possibility of the house's cut), because one wins exactly the amount one's opponents lose. Other zero sum games include matching pennies and most classical board games including go and chess. Many games studied by game theorists (including the famous prisoner's dilemma) are non-zero-sum games, because some outcomes have net results greater or less than zero. Informally, in non-zero-sum games, a gain by one player does not necessarily correspond with a loss by another.

It is possible to transform any game into a (possibly asymmetric) zero-sum game by adding an additional dummy player (often called "the board"), whose losses compensate the players' net winnings.

Simultaneous and sequential

Simultaneous games are games where both players move simultaneously, or if they do not move simultaneously, the later players are unaware of the earlier players' actions (making them effectively simultaneous). Sequential games (or dynamic games) are games where later players have some knowledge about earlier actions. This need not be perfect knowledge about every action of earlier players; it might be very little information. For instance, a player may know that an earlier player did not perform one particular action, while he does not know which of the other available actions the first player actually performed.

The difference between simultaneous and sequential games is captured in the different representations discussed above. Normal form is used to represent simultaneous games, and extensive form is used to represent sequential ones.

Perfect information and imperfect information

An important subset of sequential games consists of games of perfect information. A game is one of perfect information if all players know the moves previously made by all other players. Thus, only sequential games can be games of perfect information, since in simultaneous games not every player knows the actions of the others. Most games studied in game theory are imperfect information games, although there are some interesting examples of perfect information games, including the ultimatum game and centipede game. Perfect information games include also chess, go, mancala, and arimaa.

Perfect information is often confused with complete information, which is a similar concept. Complete information requires that every player know the strategies and payoffs of the other players but not necessarily the actions.

Infinitely long games

For obvious reasons, games as studied by economists and real-world game players are generally finished in a finite number of moves. Pure mathematicians are not so constrained, and set theorists in particular study games that last for infinitely many moves, with the winner (or other payoff) not known until after all those moves are completed.

The focus of attention is usually not so much on what is the best way to play such a game, but simply on whether one or the other player has a winning strategy. (It can be proven, using the axiom of choice, that there are games—even with perfect information, and where the only outcomes are "win" or "lose"—for which neither player has a winning strategy.) The existence of such strategies, for cleverly designed games, has important consequences in descriptive set theory.

Uses of game theory

Games in one form or another are widely used in many different academic disciplines.

Economics and business

Economists have long used game theory to analyze a wide array of economic phenomena, including auctions, bargaining, duopolies, oligopolies, social network formation, and voting systems. This research usually focuses on particular sets of strategies known as equilibria in games. These "solution concepts" are usually based on what is required by norms of rationality. The most famous of these is the Nash equilibrium. A set of strategies is a Nash equilibrium if each represents a best response to the other strategies. So, if all the players are playing the strategies in a Nash equilibrium, they have no incentive to deviate, since their strategy is the best they can do given what others are doing.

The payoffs of the game are generally taken to represent the utility of individual players. Often in modeling situations the payoffs represent money, which presumably corresponds to an individual's utility. This assumption, however, can be faulty.

A prototypical paper on game theory in economics begins by presenting a game that is an abstraction of some particular economic situation. One or more solution concepts are chosen, and the author demonstrates which strategy sets in the presented game are equilibria of the appropriate type. Naturally one might wonder to what use should this information be put. Economists and business professors suggest two primary uses.

Descriptive

The first use is to inform us about how actual human populations behave. Some scholars believe that by finding the equilibria of games they can predict how actual human populations will behave when confronted with situations analogous to the game being studied. This particular view of game theory has come under recent criticism. First, it is criticized because the assumptions made by game theorists are often violated. Game theorists may assume players always act rationally to maximize their wins (the Homo economicus model), but real humans often act either irrationally, or act rationally to maximize the wins of some larger group of people ( altruism). Game theorists respond by comparing their assumptions to those used in physics. Thus while their assumptions do not always hold, they can treat game theory as a reasonable scientific ideal akin to the models used by physicists. However, additional criticism of this use of game theory has been levied because some experiments have demonstrated that individuals do not play equilibrium strategies. For instance, in the Centipede game, Guess 2/3 of the average game, and the Dictator game, people regularly do not play Nash equilibria. There is an ongoing debate regarding the importance of these experiments.

Alternatively, some authors claim that Nash equilibria do not provide predictions for human populations, but rather provide an explanation for why populations that play Nash equilibria remain in that state. However, the question of how populations reach those points remains open.

Some game theorists have turned to evolutionary game theory in order to resolve these worries. These models presume either no rationality or bounded rationality on the part of players. Despite the name, evolutionary game theory does not necessarily presume natural selection in the biological sense. Evolutionary game theory includes both biological as well as cultural evolution and also models of individual learning (for example, fictitious play dynamics).

Normative analysis

	Cooperate	Defect
Cooperate	2, 2	0, 3
Defect	3, 0	1, 1
The Prisoner's Dilemma

On the other hand, some scholars see game theory not as a predictive tool for the behaviour of human beings, but as a suggestion for how people ought to behave. Since a Nash equilibrium of a game constitutes one's best response to the actions of the other players, playing a strategy that is part of a Nash equilibrium seems appropriate. However, this use for game theory has also come under criticism. First, in some cases it is appropriate to play a non-equilibrium strategy if one expects others to play non-equilibrium strategies as well. For an example, see Guess 2/3 of the average.

Second, the Prisoner's Dilemma presents another potential counterexample. In the Prisoner's Dilemma, each player pursuing his own self-interest leads both players to be worse off than had they not pursued their own self-interests. Some scholars believe that this demonstrates the failure of game theory as a recommendation for behaviour.

Applications in Biology

	Hawk	Dove
Hawk	v−c, v−c	2v, 0
Dove	0, 2v	v, v
The hawk-dove game

Unlike economics, the payoffs for games in biology are often interpreted as corresponding to fitness. In addition, the focus has been less on equilibria that correspond to a notion of rationality, but rather on ones that would be maintained by evolutionary forces. The most well-known equilibrium in biology is known as the Evolutionary stable strategy or (ESS), and was first introduced by John Maynard Smith (described in his 1982 book). Although its initial motivation did not involve any of the mental requirements of the Nash equilibrium, every ESS is a Nash equilibrium.

In biology, game theory has been used to understand many different phenomena. It was first used to explain the evolution (and stability) of the approximate 1:1 sex ratios. Ronald Fisher (1930) suggested that the 1:1 sex ratios are a result of evolutionary forces acting on individuals who could be seen as trying to maximize their number of grandchildren.

Additionally, biologists have used evolutionary game theory and the ESS to explain the emergence of animal communication ( Maynard Smith & Harper, 2003). The analysis of signaling games and other communication games has provided some insight into the evolution of communication among animals.

Finally, biologists have used the hawk-dove game (also known as chicken) to analyze fighting behaviour and territoriality.

Computer science and logic

Game theory has come to play an increasingly important role in logic and in computer science. Several logical theories have a basis in game semantics. In addition, computer scientists have used games to model interactive computations.

Political science

The application of game theory to political science is focused in the overlapping areas of political economy, public choice, positive political theory, and social choice theory. In each of these areas, researchers have developed game theoretic models in which the players are often voters, states, interest groups, and politicians.

For early examples of game theory applied to political science, see the work of Anthony Downs. In his book An Economic Theory of Democracy (1957), he applies a Hotelling firm location model to the political process. In the Downsian model, political candidates commit to ideologies on a one-dimensional policy space. He shows how the political candidates will converge to the ideology preferred by the median voter. For more recent examples, see the books by Gene M. Grossman and Elhanan Helpman, or David Austen-Smith and Jeffrey S. Banks.

A game-theoretic explanation for the democratic peace is that the public and open debate in democracies send clear and reliable information regarding the intentions to other states. In contrast, it is difficult to know the intentions of nondemocratic leaders, what effect concessions will have, and if promises will be kept. Thus there will be mistrust and unwillingness to make concessions if at least one of the parties in a dispute is a nondemocracy.

Philosophy

	Stag	Hare
Stag	3, 3	0, 2
Hare	2, 0	2, 2
Stag hunt

Game theory has been put to several uses in philosophy. Responding to two papers by W.V.O. Quine (1960, 1967), David Lewis (1969) used game theory to develop a philosophical account of convention. In so doing, he provided the first analysis of common knowledge and employed it in analyzing play in coordination games. In addition, he first suggested that one can understand meaning in terms of signaling games. This later suggestion has been pursued by several philosophers since Lewis (Skyrms 1996, Grim et al. 2004).

In ethics, some authors have attempted to pursue the project, begun by Thomas Hobbes, of deriving morality from self-interest. Since games like the Prisoner's Dilemma present an apparent conflict between morality and self-interest, explaining why cooperation is required by self-interest is an important component of this project. This general strategy is a component of the general social contract view in political philosophy (for examples, see Gauthier 1987 and Kavka 1986).

Finally, other authors have attempted to use evolutionary game theory in order to explain the emergence of human attitudes about morality and corresponding animal behaviors. These authors look at several games including the Prisoner's Dilemma, Stag hunt, and the Nash bargaining game as providing an explanation for the emergence of attitudes about morality (see, e.g., Skyrms 1996, 2004; Sober and Wilson 1999).

Sociology

There are fewer applications of game theory in sociology than in its sister disciplines, economics and political science. A game theoretic analysis of interactions among prisoners is conducted by Kaminski (2004).

History of game theory

The first known discussion of game theory occurred in a letter written by James Waldegrave in 1713. In this letter, Waldegrave provides a minimax mixed strategy solution to a two-person version of the card game le Her. It was not until the publication of Antoine Augustin Cournot's Researches into the Mathematical Principles of the Theory of Wealth in 1838 that a general game theoretic analysis was pursued. In this work Cournot considers a duopoly and presents a solution that is a restricted version of the Nash equilibrium.

Although Cournot's analysis is more general than Waldegrave's, game theory did not really exist as a unique field until John von Neumann published a series of papers in 1928. While the French mathematician Borel did some earlier work on games, von Neumann can rightfully be credited as the inventor of game theory. Von Neumann was a brilliant mathematician whose work was far-reaching from set theory to his calculations that were key to development of both the Atom and Hydrogen bombs and finally to his work developing computers. Von Neumann's work culminated in the 1944 book The Theory of Games and Economic Behaviour by von Neumann and Oskar Morgenstern. This profound work contains the method for finding optimal solutions for two-person zero-sum games. During this time period, work on game theory was primarily focused on cooperative game theory, which analyzes optimal strategies for groups of individuals, presuming that they can enforce agreements between them about proper strategies.

In 1950, the first discussion of the Prisoner's dilemma appeared, and an experiment was undertaken on this game at the RAND corporation. Around this same time, John Nash developed a definition of an "optimum" strategy for multiplayer games where no such optimum was previously defined, known as Nash equilibrium. This equilibrium is sufficiently general, allowing for the analysis of non-cooperative games in addition to cooperative ones.

Game theory experienced a flurry of activity in the 1950s, during which time the concepts of the core, the extensive form game, fictitious play, repeated games, and the Shapley value were developed. In addition, the first applications of Game theory to philosophy and political science occurred during this time.

In 1965, Reinhard Selten introduced his solution concept of subgame perfect equilibria, which further refined the Nash equilibrium (later he would introduce trembling hand perfection as well). In 1967, John Harsanyi developed the concepts of complete information and Bayesian games. He, along with John Nash and Reinhard Selten, won the Bank of Sweden Prize in Economic Sciences in Memory of Alfred Nobel in 1994.

In the 1970s, game theory was extensively applied in biology, largely as a result of the work of John Maynard Smith and his evolutionary stable strategy. In addition, the concepts of correlated equilibrium, trembling hand perfection, and common knowledge were introduced and analyzed.

In 2005, game theorists Thomas Schelling and Robert Aumann won the Bank of Sweden Prize in Economic Sciences. Schelling worked on dynamic models, early examples of evolutionary game theory. Aumann contributed more to the equilibrium school, developing an equilibrium coarsening correlated equilibrium and developing extensive analysis of the assumption of common knowledge.