Ptolemy
2007 Schools Wikipedia Selection. Related subjects: Astronomers and physicists
Claudius Ptolemaeus ( Greek: Κλαύδιος Πτολεμαῖος; c. 90 – c. 168 AD), known in English as Ptolemy, was a Greek mathematician, geographer, astronomer, and astrologer who lived in the Hellenistic culture of Roman Egypt. Although no description of his family background or physical appearance exists, it is likely he was born in Egypt, probably in or near Alexandria.
Ptolemy was the author of several scientific treatises, three of which would be of continuing importance to later Islamic and European science. The first is the astronomical treatise that is now known as the Almagest (in Greek Η μεγάλη Σύνταξις , "The Great Treatise"). The second is the Geography, which is a thorough discussion of the geographic knowledge of the Greco-Roman world. The third is the astrological treatise known as the Tetrabiblos ("Four books") in which he attempted to adapt horoscopic astrology to the Aristotelian natural philosophy of his day.
Name
Claudius is a Roman name. Claudius Ptolemy was almost certainly a Roman citizen, and he or his ancestor adopted the nomen of a Roman called Claudius, who was in some sense responsible for the citizenship. If, as was not uncommon, this Roman was the Emperor, the citizenship would have been granted between 14 and 68 CE. The astronomer would also have had a praenomen, which we do not know.
Ptolemy is a Greek name. It occurs once in Greek mythology, and is of Homeric form. It was quite common among the Macedonian upper class at the time of Alexander the Great, and there are several among Alexander's army, one of whom made himself King of Egypt; all the Kings after him, until Rome conquered Egypt, were also Ptolemies. Whether the astronomer's name represents royal blood, loyalty, or chance is also not known.
Ptolemy read, and wrote in, Greek; he used Babylonian data, probably in translation. He worked in Alexandria, which was a primarily Greek and Jewish city on the edge of Egypt; there is relatively little evidence of native Egyptian inhabitants.
Astronomy
In the Almagest, one of the most influential books of classical antiquity, Ptolemy compiled and extended the astronomical knowledge and theories of the ancient Greek and Babylonian world; he relied mainly on the work of Hipparchus of three centuries earlier. It was preserved, like most of Classical Greek science, in Arabic manuscripts (hence its familiar name) and only made available in Latin translation (by Gerard of Cremona) in the 12th century. Ptolemy formulated a geocentric model that was widely accepted until it was superseded by the heliocentric solar system of Copernicus. Likewise his computational methods (supplemented in the 12th century with the Arabic computational Tables of Toledo) were of sufficient accuracy to satisfy the needs of astronomers, astrologers and navigators, until the time of the great explorations. They were also adopted in the Arab world and in India. The Almagest also contains a star catalogue, which is probably an updated version of a catalogue created by Hipparchus. Its list of forty-eight constellations is ancestral to the modern system of constellations, but unlike the modern system they did not cover the whole sky (only the sky Ptolemy could see). The Almagest is also known as the Great Syntaxis of Astronomy.
Ptolemy's astronomy has been wideley criticized for its incorrect geocentric view. But according to Manly Hall, an expert on arcane wisdom traditions and occult mathematics and science, this was meant to describe man's spiritual nature, not the actual astronomical scheme of the universe, he wrote "in ridiculing the geocentric system of astronomy expounded by Claudius Ptolemy, modern astronomers have overlooked the philosophic key to the Ptolemaic system. The universe of Ptolemy is a diagram of the relationships existing between the various divine and elemental parts of every creature, and is not concerned with astronomy as that science is now comprehended. In the above figure, special attention is called to the three circles of zodiacs surrounding the orbits of the planets. These zodiacs represent the threefold spiritual constitution of the universe. The orbits of the planets are the Governors of the World and the four elemental spheres in the centre represent the physical constitution of both man and the universe. Ptolemy's scheme of the universe is a cross section of the universal aura, the planets and elements to which he refers having no relation to those recognized by modern astronomers." (source: http://prs.org/gallery-classic.htm).
In the Phaseis (Risings of the Fixed Stars) Ptolemy gave a parapegma, a star calendar or almanac based on the appearances and disappearances of stars over the course of the solar year.
Geographia
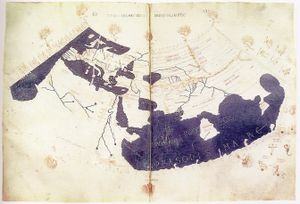
Ptolemy's other main work is his Geographia. This too is a compilation of what was known about the world's geography in the Roman Empire during his time. He relied mainly on the work of an earlier geographer, Marinos of Tyre, and on gazetteers of the Roman and ancient Persian Empire, but most of his sources beyond the perimeter of the Empire were unreliable.
The first part of the Geographia is a discussion of the data and of the methods he used. Like with the model of the solar system in the Almagest, Ptolemy put all this information into a grand scheme. He assigned coordinates to all the places and geographic features he knew, in a grid that spanned the globe. Latitude was measured from the equator, as it is today, but Ptolemy preferred to express it as the length of the longest day rather than degrees of arc (the length of the midsummer day increases from 12h to 24h as you go from the equator to the polar circle). He put the meridian of 0 longitude at the most western land he knew, the Canary Islands.
Ptolemy also devised and provided instructions on how to create maps both of the whole inhabited world (oikoumenè) and of the Roman provinces. In the second part of the Geographia he provided the necessary topographic lists, and captions for the maps. His oikoumenè spanned 180 degrees of longitude from the Canary islands in the Atlantic Ocean to the middle of China, and about 80 degrees of latitude from the Arctic to the East Indies and deep into Africa; Ptolemy was well aware that he knew about only a quarter of the globe, and he knew that his information did not extend to the Eastern Sea.
The maps in surviving manuscripts of Ptolemy's Geographia, however, date only from about 1300, after the text was rediscovered by Maximus Planudes. It seems likely that the topographical tables in books 2-7 are cumulative texts - texts which were altered and added to as new knowledge became available in the centuries after Ptolemy (Bagrow 1945). This means that information contained in different parts of the Geography is likely to be of different date.
Maps based on scientific principles had been made since the time of Eratosthenes ( 3rd century BC), but Ptolemy improved projections. It is known that a world map based on the Geographia was on display in Autun, France in late Roman times. In the 15th century Ptolemy's Geographia began to be printed with engraved maps; the earliest printed edition with engraved maps was produced in Bologna in 1477, followed quickly by a Roman edition in 1478 (Campbell, 1987). An edition printed at Ulm in 1482, including woodcut maps, was the first one printed north of the Alps. The maps look distorted as compared to modern maps, because Ptolemy's data were inaccurate. One reason is that Ptolemy estimated the size of the Earth as too small: while Eratosthenes found 700 stadia for a degree on the globe, in the Geographia Ptolemy uses 500 stadia. It is not certain if these geographers used the same stadion. If they both used the traditional Attic stadion of about 185 meters, then the older estimate is 1/6 too large, and Ptolemy's value is 1/6 too small. See also Ancient Greek units of measurement and History of geodesy.
Because Ptolemy derived most of his topographic coordinates by converting measured distances to angles, his maps get distorted. So his values for the latitude were in error by up to 2 degrees. For longitude this was even worse, because there was no reliable method to determine geographic longitude; Ptolemy was well aware of this. It remained a problem in geography until the invention of chronometers at the end of the 18th century. It must be added that his original topographic list cannot be reconstructed: the long tables with numbers were transmitted to posterity through copies containing many scribal errors, and people have always been adding or improving the topographic data: this is a testimony to the persistent popularity of this influential work in the history of cartography.
Astrology
Ptolemy's treatise on astrology, the Tetrabiblos, was the most popular astrological work of antiquity and also enjoyed great influence in the Islamic world and the medieval Latin West. The Tetrabiblos is an extensive and continually reprinted treatise on the ancient principles of Horoscopic astrology in four books (Greek tetra means "four", biblos is "book"). That it did not quite attain the unrivalled status of the Syntaxis was perhaps because it did not cover some popular areas of the subject, particularly electional astrology (interpreting astrological charts for a particular moment to determine the outcome of a course of action to be initiated at that time), and medical astrology.
The great popularity that the Tetrabiblos did possess might be attributed to its nature as an exposition of the art of astrology and as a compendium of astrological lore, rather than as a manual. It speaks in general terms, avoiding illustrations and details of practice. Ptolemy was concerned to defend astrology by defining its limits, compiling astronomical data that he believed was reliable and dismissing practices (such as considering the numerological significance of names) that he believed to be without sound basis.
Much of the content of the Tetrabiblos may well have been collected from earlier sources; Ptolemy's achievement was to order his material in a systematic way, showing how the subject could, in his view, be rationalized. It is, indeed, presented as the second part of the study of astronomy of which the Syntaxis was the first, concerned with the influences of the celestial bodies in the sublunar sphere. Thus explanations of a sort are provided for the astrological effects of the planets, based upon their combined effects of heating, cooling, moistening, and drying.
Ptolemy's astrological outlook was quite practical: he thought that astrology was like medicine, that is conjectural, because of the many variable factors to be taken into account: the race, country, and upbringing of a person affects an individual's personality as much if not more than the positions of the Sun, Moon, and planets at the precise moment of their birth, so Ptolemy saw astrology as something to be used in life but in no way relied on entirely.
Music
Ptolemy also wrote an influential work, Harmonics, on music theory and the mathematics of music. After criticizing the approaches of his predecessors, Ptolemy argued for basing musical intervals on mathematical ratios (in contrast to the followers of Aristoxenus and in agreement with the followers of Pythagoras) backed up by empirical observation (in contrast to the overly-theoretical approach of the Pythagoreans). Ptolemy wrote about how musical notes could be translated into mathematical equations and vice versa in Harmonics. This is called Pythagorean tuning because it was first discovered by Pythagoras. However, Pythagoras believed that the mathematics of music should be based on the specific ratio of 3:2 whereas Ptolemy merely believed that it should just generally involve tetrachords and octaves. He presented his own divisions of the tetrachord and the octave, which he derived with the help of a monochord. Ptolemy's astronomical interests also appeared in a discussion of the music of the spheres.
Other works
In his Optics, a work which survives only in a poor Arabic translation, he writes about properties of light, including reflection, refraction and colour. The work is a significant part of the early history of optics. His other works include Planetary Hypothesis, Planisphaerium and Analemma.
Named after Ptolemy
- Ptolemaeus crater on the Moon.
- Ptolemaeus crater on Mars.
- The asteroid 4001 Ptolemaeus.
- A character in the fantasy series The Bartimaeus Trilogy.