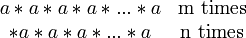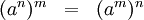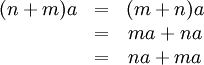Elementary group theory

2007 Schools Wikipedia Selection. Related subjects: Mathematics

In mathematics, a group (G,*) is usually defined as:

G is a set and * is an associative binary operation on G, obeying the following rules (or axioms):

A1. ( Closure) If a and b are in G, then a*b is in G

A2. ( Associativity) If a, b, and c are in G, then (a*b)*c=a*(b*c).

A3. ( Identity) G contains an element, often denoted e, such that for all a in G, a*e=e*a=a. We call this element the identity of (G,*). (We will show e is unique later.)

A4. ( Inverses) If a is in G, then there exists an element b in G such that a*b=b*a=e. We call b the inverse of a. (We will show b is unique later.)

Closure and associativity are part of the definition of "associative binary operation", and are sometimes omitted, particularly closure.

Notes:

The * is not necessarily multiplication. Addition works just as well, as do many less standard operations.
When * is a standard operation, we use the standard symbol instead (for example, + for addition).
When * is addition or any commutative operation (except multiplication), the identity is usually denoted by 0 and the inverse of a by -a. The operation is always denoted by something other than *, often +, to avoid confusion with multiplication.
When * is multiplication or any non-commutative operation, the identity is usually denoted by 1 and the inverse of a by a^-1. The operation is often omitted, a*b is often written ab.
(G,*) is usually pronounced "the group G under *". When affirming that it is a group (for example, in a theorem), we say that "G is a group under *".
The group (G,*) is often referred to as "the group G" or simply "G"; but the operation "*" is fundamental to the description of the group.

Examples

(R,+) is a group

The real numbers (R) are a group under addition (+).

Closure: Clear; adding any two numbers gives another number.

Associativity: Clear; for any a, b, c in R, (a+b)+c=a+(b+c).

Identity: 0. For any a in R, a+0=a. (Hence the denotation 0 for identity)

Inverses: For any a in R, -a+a=0. (Hence the denotation -a for inverse)

(R,*) is not a group

The real numbers (R) are NOT a group under multiplication (*).

Identity: 1.

Inverses: 0*a=0 for all a in R, so 0 has no inverse.

(R^#,*) is a group

The real numbers without 0 (R^#) are a group under multiplication (*).

Closure: Clear; multiplying any two numbers gives another number.

Associativity: Clear; for any a, b, c in R, (a*b)*c=a*(b*c).

Identity: 1. For any a in R, a*1=a. (Hence the denotation 1 for identity)

Inverses: For any a in R, a^-1*a=1. (Hence the denotation a^-1 for inverse)

Basic theorems

Inverse relations are commutative

Theorem 1.1: For all a in G, a^-1*a = e.

By expanding a^-1*a, we get
- a^-1*a = a^-1*a*e (by A3')
- a^-1*a*e = a^-1*a*(a^-1*(a^-1)^-1) (by A4', a^-1 has an inverse denoted (a^-1)^-1)
- a^-1*a*(a^-1*(a^-1)^-1) = a^-1*(a*a^-1)*(a^-1)^-1 = a^-1*e*(a^-1)^-1 (by associativity and A4')
- a^-1*e*(a^-1)^-1 = a^-1*(a^-1)^-1 = e (by A3' and A4')
Therefore, a^-1*a = e

Identity relations are commutative

Theorem 1.2: For all a in G, e*a = a.

Expanding e*a,
- e*a = (a*a^-1)*a (by A4)
- (a*a^-1)*a = a*(a^-1*a) = a*e (by associativity and the previous theorem)
- a*e = a (by A3)
Therefore e*a = a

Latin square property

Theorem 1.3: For all a,b in G, there exists a unique x in G such that a*x = b.

Certainly, at least one such x exists, for if we let x = a^-1*b, then x is in G (by A1, closure); and then
- a*x = a*(a^-1*b) (substituting for x)
- a*(a^-1*b) = (a*a^-1)*b (associativity A2).
- (a*a^-1)*b= e*b = b. (identity A3).
- Thus an x always exists satisfying a*x = b.
To show that this is unique, if a*x=b, then
- x = e*x
- e*x = (a^-1*a)*x
- (a^-1*a)*x = a^-1*(a*x)
- a^-1*(a*x) = a^-1*b
- Thus, x = a^-1*b

Similarly, for all a,b in G, there exists a unique y in G such that y*a = b.

The identity is unique

Theorem 1.4: The identity element of a group (G,*) is unique.

a*e = a (by A3)
Apply theorem 1.3, with b = a.

Alternative proof: Suppose that G has two identity elements, e and f say. Then e*f = e, by A3', but also e*f = f, by Theorem 1.2. Hence e = f.

As a result, we can speak of the identity element of (G,*) rather than an identity element. Where different groups are being discussed and compared, often e_G will be used to identify the identity in (G,*).

Inverses are unique

Theorem 1.5: The inverse of each element in (G,*) is unique; equivalently, for all a in G, a*x = e if and only if x=a^-1.

If x=a^-1, then a*x = e by A4.
Apply theorem 1.3, with b = e.

Alternative proof: Suppose that an element g of G has two inverses, h and k say. Then h = h*e = h*(g*k) = (h*g)*k = e*k = k (equalities justified by A3'; A4'; A2; Theorem 1.1; and Theorem 1.2, respectively).

As a result, we can speak of the inverse of an element x, rather than an inverse.

Inverting twice gets you back where you started

Theorem 1.6: For all a belonging to a group (G,*), (a^-1)^-1=a.

a^-1*a = e.
Therefore the conclusion follows from theorem 1.4.

The inverse of ab

Theorem 1.7: For all a,b belonging to a group (G,*), (a*b)^-1=b^-1*a^-1.

(a*b)*(b^-1*a^-1) = a*(b*b^-1)*a^-1 = a*e*a^-1 = a*a^-1 = e
Therefore the conclusion follows from theorem 1.4.

Cancellation

Theorem 1.8: For all a,x,y, belonging to a group (G,*), if a*x=a*y, then x=y; and if x*a=y*a, then x=y.

If a*x = a*y then:
- a^-1*(a*x) = a^-1*(a*y)
- (a^-1*a)*x = (a^-1*a)*y
- e*x = e*y
- x = y
If x*a = y*a then
- (x*a)*a^-1 = (y*a)*a^-1
- x*(a*a^-1) = y*(a*a^-1)
- x*e = y*e
- x = y

Repeated use of *

Theorem 1.9: For every a in a group (G,*), we define

$\begin{matrix}&a*a*a*a*...*a&\mbox{m times}\\ &*a*a*a*...*a&\mbox{n times}\end{matrix}$

as :

$\begin{matrix} a^m*a^n &=& a^{m+n}\\ &=& a^n*a^m \end{matrix}$

and

$\begin{matrix} (a^n)^m&=& (a^m)^n \end{matrix}$

and

$\begin{matrix} a^{-n}= a^{-1}*a^{-1}*a^{-1}*...*a^{-1} &\mbox{n times} \end{matrix}$

However, when the operation is noted +, we note

$\begin{matrix}&a+a+a+a+...+a&\mbox{m times}\\ &+a+a+a+...+a&\mbox{n times}\end{matrix}$

as :

$\begin{matrix} (n+m)a&=& (m+n)a\\ &=& ma+na\\ &=& na+ma \end{matrix}$

and

$\begin{matrix} -na = (-a)+(-a)+(-a)+(-a)+...+(-a) &\mbox{n times} \end{matrix}$

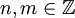Where $n,m \in \mathbb{Z}$ (This generalizes the associativity.)

Groups in which all non-trivial elements have order 2

Theorem 1.10: A group where all non-trivial elements have order 2 is abelian. In other words, if all elements g in a group G satisfy g*g=e, then for any 2 elements g, h in G, g*h=h*g.

Let g, h be any 2 elements in a group G
By A1, g*h is also a member of G
Using the given condition, we know (g*h)*(g*h)=e. Now
- g*(g*h)*(g*h) = g*e
- g*(g*h)*(g*h)*h = g*e*h
- (g*g)*(h*g)*(h*h) = (g*e)*h
- e*(h*g)*e = g*h
- h*g = g*h
Since the group operation commutes, the group is abelian

Definitions

Given a group (G, *), if the total number of elements in G is finite, then the group is called a finite group. The order of a group (G,*) is the number of elements in G (for a finite group), or the cardinality of the group if G is not finite. The order of a group G is written as |G| or (less frequently) o(G).

A subset H of G is called a subgroup of a group (G,*) if H satisfies the axioms of a group, using the same operator "*", and restricted to the subset H. Thus if H is a subgroup of (G,*), then (H,*) is also a group, and obeys the above theorems, restricted to H. The order of subgroup H is the number of elements in H.

A proper subgroup of a group G is a subgroup which is not identical to G. A non-trivial subgroup of G is (usually) any proper subgroup of G which contains an element other than e.

Theorem 2.1: If H is a subgroup of (G,*), then the identity e_H in H is identical to the identity e in (G,*).

If h is in H, then h*e_H = h; since h must also be in G, h*e = h; so by theorem 1.4, e_H = e.

Theorem 2.2: If H is a subgroup of G, and h is an element of H, then the inverse of h in H is identical to the inverse of h in G.

Let h and k be elements of H, such that h*k = e; since h must also be in G, h*h^-1 = e; so by theorem 1.5, k = h^-1.

Given a subset S of G, we often want to determine whether or not S is also a subgroup of G. One handy theorem that covers the case for both finite and infinite groups is:

Theorem 2.3: If S is a non-empty subset of G, then S is a subgroup of G if and only if for all a,b in S, a*b^-1 is in S.

If for all a, b in S, a*b^-1 is in S, then
- e is in S, since a*a^-1 = e is in S.
- for all a in S, e*a^-1 = a^-1 is in S
- for all a, b in S, a*b = a*(b^-1)^-1 is in S
- Thus, the axioms of closure, identity, and inverses are satisfied, and associativity is inherited; so S is subgroup.
Conversely, if S is a subgroup of G, then it obeys the axioms of a group.
- As noted above, the identity in S is identical to the identity e in G.
- By A4, for all b in S, b^-1 is in S
- By A1, a*b^-1 is in S.

The intersection of two or more subgroups is again a subgroup.

Theorem 2.4: The intersection of any non-empty set of subgroups of a group G is a subgroup.

Let {H_i} be a set of subgroups of G, and let K = ∩{H_i}.
e is a member of every H_i by theorem 2.1; so K is not empty.
If h and k are elements of K, then for all i,
- h and k are in H_i.
- By the previous theorem, h*k^-1 is in H_i
- Therefore, h*k^-1 is in ∩{H_i}.
Therefore for all h, k in K, h*k^-1 is in K.
Then by the previous theorem, K=∩{H_i} is a subgroup of G; and in fact K is a subgroup of each H_i.

In a group (G,*), define x⁰ = e. We write x*x as x² ; and in general, x*x*x*...*x (n times) as xⁿ. Similarly, we write x^-n for (x^-1)ⁿ.

Theorem 2.5: Let a be an element of a group (G,*). Then the set {aⁿ: n is an integer} is a subgroup of G.

A subgroup of this type is called a cyclic subgroup; the subgroup of the powers of a is often written as <a>, and we say that a generates <a>.

If there exists a positive integer n such that aⁿ=e, then we say the element a has order n in G where n is the smallest n. Sometimes this is written as "o(a)=n".

If S and T are subsets of G, and a is an element of G, we write "a*S" to refer to the subset of G made up of all elements of the form a*s, where s is an element of S; similarly, we write "S*a" to indicate the set of elements of the form s*a. We write S*T for the subset of G made up of elements of the form s*t, where s is an element of S and t is an element of T.

If H is a subgroup of G, then a left coset of H is a set of the form a*H, for some a in G. A right coset is a subset of the form H*a.

Some useful theorems about cosets, stated without proof:

Theorem: If H is a subgroup of G, and x and y are elements of G, then either x*H = y*H, or x*H and y*H have empty intersection.

Theorem: If H is a subgroup of G, every left (right) coset of H in G contains the same number of elements.

Theorem: If H is a subgroup of G, then G is the disjoint union of the left (right) cosets of H.

Theorem: If H is a subgroup of G, then the number of distinct left cosets of H is the same as the number of distinct right cosets of H.

Define the index of a subgroup H of a group G (written "[G:H]") to be the number of distinct left cosets of H in G.

From these theorems, we can deduce the important Lagrange's theorem relating the order of a subgroup to the order of a group:

Lagrange's theorem: If H is a subgroup of G, then |G| = |H|*[G:H].

For finite groups, this also allows us to state:

Lagrange's theorem: If H is a subgroup of a finite group G, then the order of H divides the order of G.

Theorem: If the order of a group G is a prime number, then the group is cyclic.

Retrieved from " http://en.wikipedia.org/wiki/Elementary_group_theory"